✉️ Fractions support in Scalar Calculator

When working with Scalar you can enter numbers in the form of fractions and convert decimal numbers into fractions. This is very convenient because fractions function on a par with other numbers, i.e. they are converted to decimal numbers.

⭐ Entering number as fractions

Entering numbers in the form of fractions is done using the following syntax:

• a_b  : a – numerator, b – denominator, converted to decimal: a/b
• a_b_c : a – whole, b – numerator, c – denominator, converted to decimal: a+c/b

Please follow the below example:

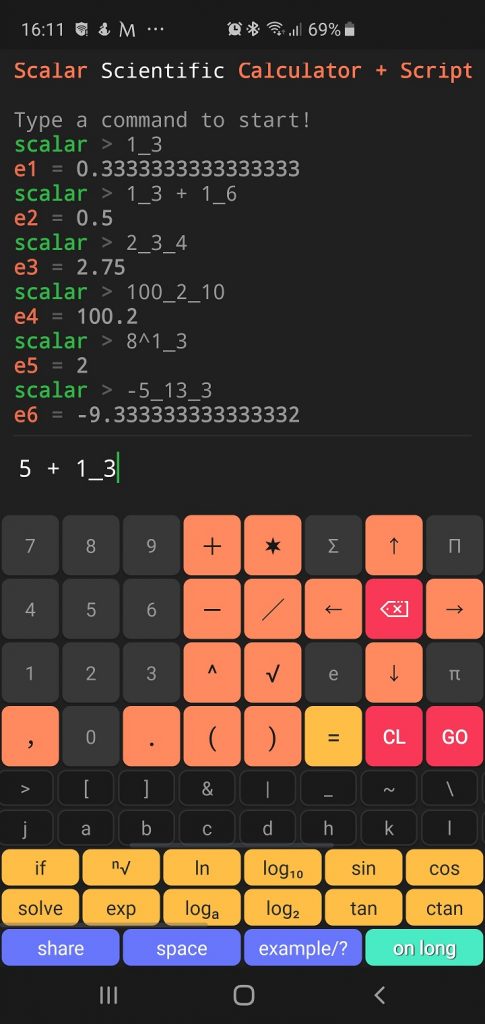
Scalar code result:

scalar > 1_3
e1 = 0.3333333333333333
scalar > 1_3 + 1_6
e2 = 0.5
scalar > 2_3_4
e3 = 2.75
scalar > 100_2_10
e4 = 100.2
scalar > 8^1_3
e5 = 2
scalar > -5_13_3
e6 = -9.333333333333332

Scalar script:

1_3
1_3 + 1_6
2_3_4
100_2_10
8^1_3
-5_13_3

⭐ Converting decimal to fraction

Result of any expression can be presented as a fraction. Please use below syntax:

frac expression

The conversion procedure in some cases may give an approximate result. That is why it is worth observing the epsilon parameter.

Please follow below examples:

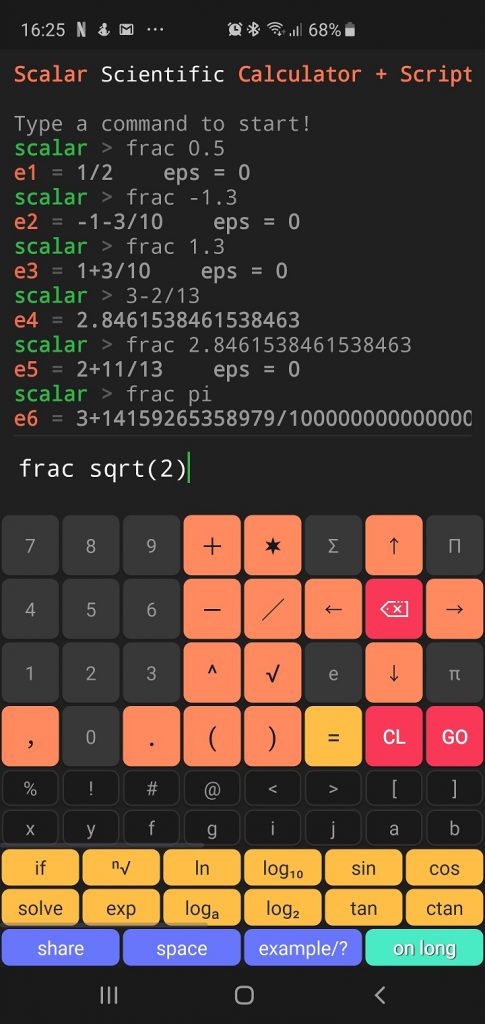
Scalar code result:

scalar > frac 0.5
e1 = 1/2    eps = 0
scalar > frac -1.3
e2 = -1-3/10    eps = 0
scalar > frac 1.3
e3 = 1+3/10    eps = 0
scalar > 3-2/13
e4 = 2.8461538461538463
scalar > frac 2.8461538461538463
e5 = 2+11/13    eps = 0
scalar > frac pi
e6 = 3+14159265358979/100000000000000    eps = 0.0000000000000031086244689504383

Scalar script:

frac 0.5
frac -1.3
frac 1.3
3-2/13
frac 2.8461538461538463
frac pi

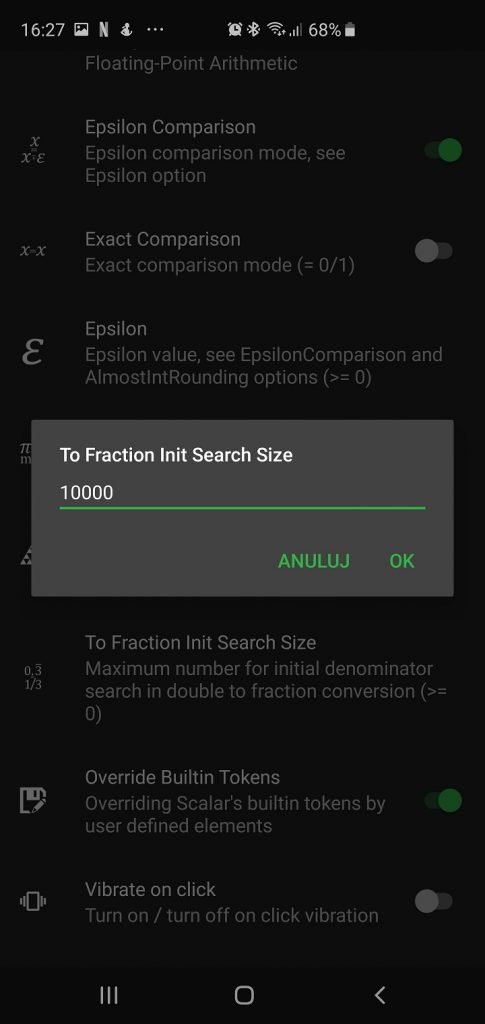
The decimal to fraction conversion algorithm is carried out in a few steps. The first step is to try to find an accurate representation through an optimized search method. You can control the search range using the parameter available in the application options.

To Fraction Init Search Size – Maximum number for initial search of denominator – default value 10000

Thank you 🙂

Thank you for reading and thank you for using Scalar. If you like my app please make me a gift posting a review on Google Play store – links below.

Scalar in action

Scalar Free

Scalar Pro

All the best!