Today I will present various types of support for prime numbers that the Scalar calculator provides. There will be some theory, some screenshots, and a few lines of code that you can use directly in your Scalar instances. Stay tuned! 🙂
⭐ Scalar functions and options related to prime numbers
Let’s start with the list of functions and options available in Scalar, which are linked to prime numbers. On the calculator screen, long click on the “example /?” button. As a result you will get the help dialog containing search option. Enter “prime” keyword.

Scalar functions list:
- ispr(n) – prime number test (is number a prime?)
- Pi(n) – prime-counting function – Pi(x)
- nfact(x) – prime decomposition – number of distinct prime factors
- factval(number, factorid) – prime decomposition – factor value at position between 1 … nfact(n) – ascending order by factor value
- factexp(number, factorid) – prime decomposition – factor exponent / multiplicity at position between 1 … nfact(n) – ascending order by factor value
- factor expr – prime factorization – calculate expression, return result in the form of prime factors
- fact expr – the same as factor
⭐ Scalar – Prime test function
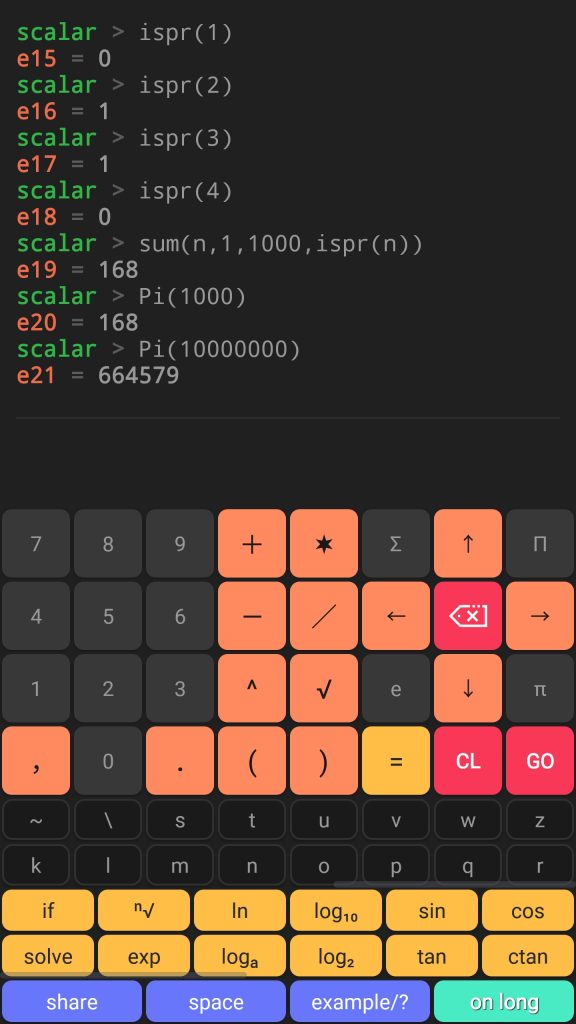
Prime test function ispr(n) returns 1 if the number is prime and 0 otherwise. Using sigma summation operator sum(arg, from, to, expr) plus combination with ispr(n) it is very easy to count primes in a given range. Please refer to the below example:
Scalar code result:
scalar > ispr(1) e15 = 0 scalar > ispr(2) e16 = 1 scalar > ispr(3) e17 = 1 scalar > ispr(4) e18 = 0 scalar > sum(n,1,1000,ispr(n)) e19 = 168 scalar > Pi(1000) e20 = 168 scalar > Pi(10000000) e21 = 664579
Scalar script:
ispr(1) ispr(2) ispr(3) ispr(4) sum(n,1,1000,ispr(n)) Pi(1000) Pi(10000000)
Above example shows also the Pi(n) prime-counting function.
⭐ Scalar – Prime-counting function
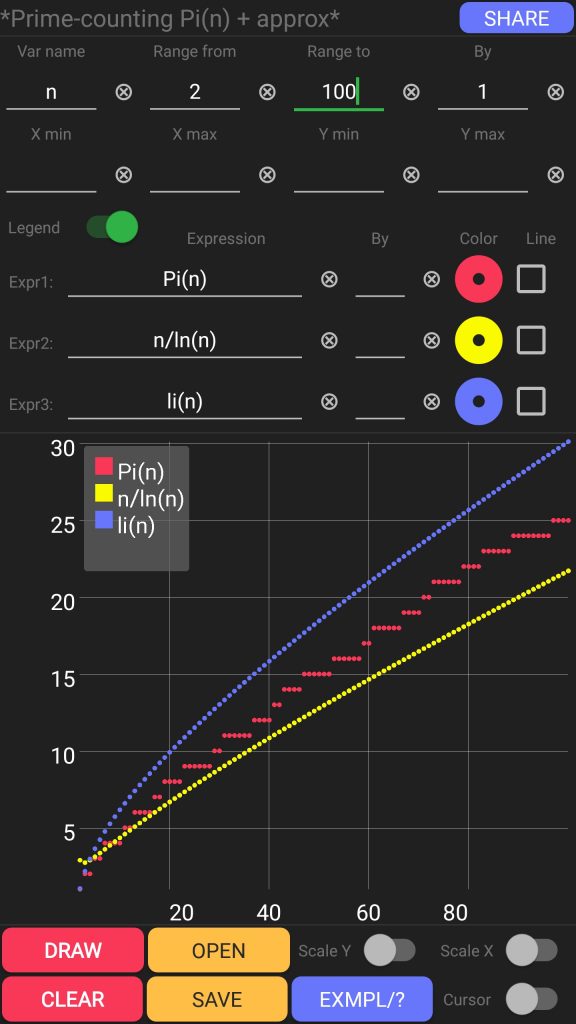
This time I will show visually the quality of various approximations of Pi(n) prime-counting function:
- Pi(n) – prime-counting function – definition can be found here,
- li(n) – logarithmic integral – a special function – please refer to the definition here,
- n/ln(n) – Gauss-Legendre approximation of Pi(n)
Prime-counting function in the range between 2 and 100
Scalar graph script:
var = n from = 2 to = 100 exp1 = Pi(n) exp2 = n/ln(n) exp3 = li(n) by = 1 curs = 1
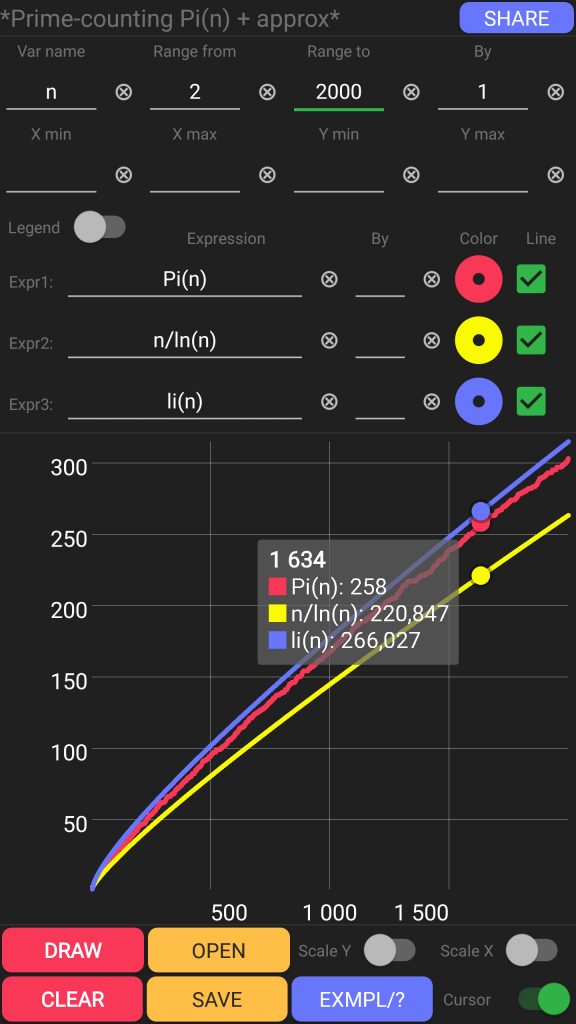
Prime-counting function in the range between 2 and 2000
Scalar graph script:
var = n from = 2 to = 2000 exp1 = Pi(n) exp2 = n/ln(n) exp3 = li(n) by = 1 curs = 1
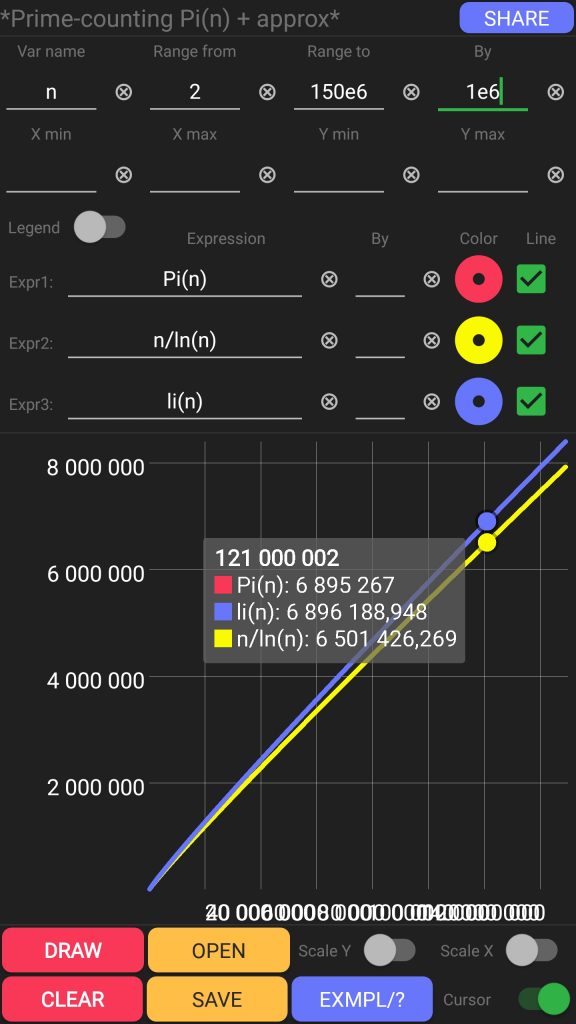
Prime-counting function in the range between 2 and 150000000
Scalar graph script:
var = n from = 2 to = 150e6 exp1 = Pi(n) exp2 = n/ln(n) exp3 = li(n) by = 1e6 curs = 1
⭐ Scalar – Prime factorization
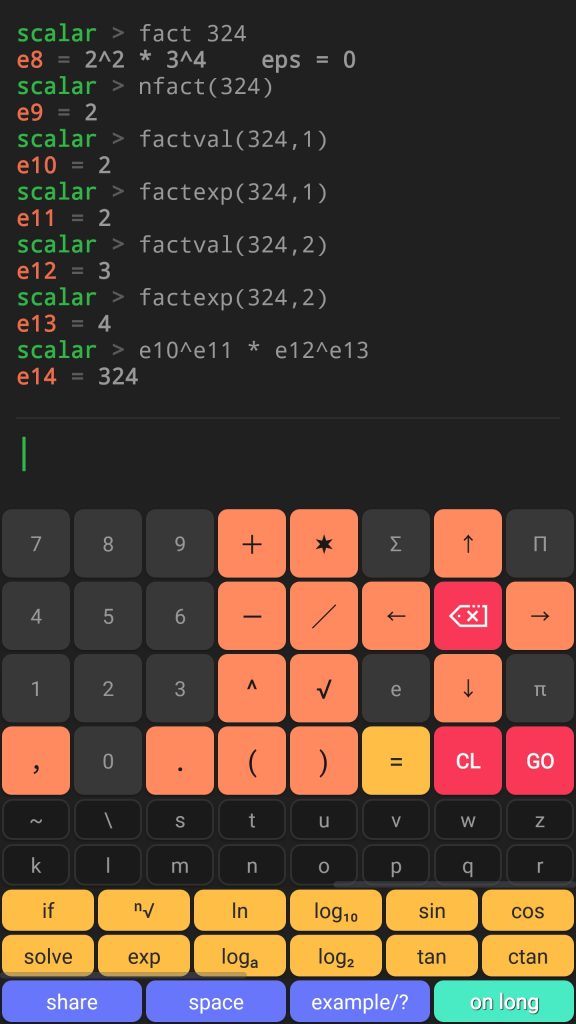
To get prime factors for a given number just use factor or fact Scalar command. Please refer to the below screenshots:
Scalar code result:
scalar > fact 324 e8 = 2^2 * 3^4 eps = 0 scalar > nfact(324) e9 = 2 scalar > factval(324,1) e10 = 2 scalar > factexp(324,1) e11 = 2 scalar > factval(324,2) e12 = 3 scalar > factexp(324,2) e13 = 4 scalar > e10^e11 * e12^e13 e14 = 324
Scalar script:
fact 324 nfact(324) factval(324,1) factexp(324,1) factval(324,2) factexp(324,2)
Scalar code result:
scalar > fact 324 e1 = 2^2 * 3^4 eps = 0 scalar > fact 254*5 e2 = 2^1 * 5^1 * 127^1 eps = 0 scalar > fact 1254685755845 e3 = 5^1 * 250937151169^1 eps = 0 scalar > n=2598 scalar > fact n e4 = 2^1 * 3^1 * 433^1 eps = 0
Scalar script:
fact 324 fact 254*5 fact 1254685755845 n=2598 fact n
⭐ Scalar – Primes cache to accelerate the calculations
Counting primes is a time consuming task.
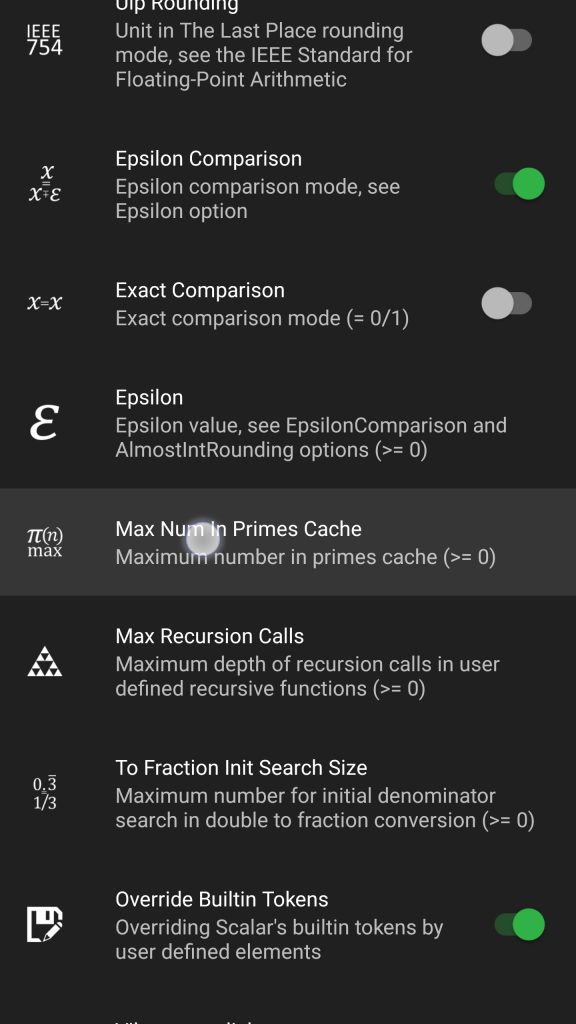
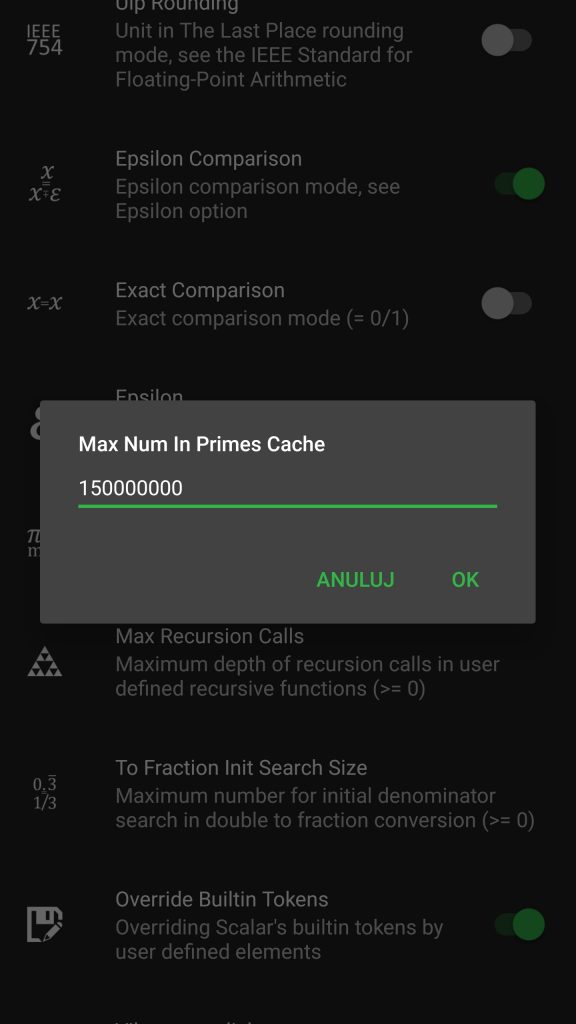
In order to significantly accelerate the calculation Scalar implements Sieve of Eratosthenes. The only thing you have to do is to go to the settings screen and enter in the “Max num in primes cache” option the range that will be examined. After doing so, Scalar will build the cache that will be saved in memory for further usage.
Say bye bye for prolonging progress bar! 🙂
? Scalar in action
? Scalar Free

? Scalar Pro

Best regards! 🙂