Recently, I was thinking about various justifications for the definition of 0! (factorial of zero) which is
$$0!=1$$
The assumed value of 1 may seem quite obvious if you consider the recursive formula. However, it did not satisfy me “mathematically”. That’s why I decided to write these few sentences. I will give motivations for the less advanced ones, but there will also be motivations for slightly more insiders.
⭐️Factorial in Scalar Calculator
⭐️ Factorial and recurrence
For integer n > 0 factorial is defined as follows
$$n!=n\times (n-1)\times (n-2)\times \ldots \times 2\times 1$$
With ease you can see that below recursive formula follows
$$n!=n\times (n-1)!$$
$$1!=1$$
⭐️ 0! = 1 – motivation based on recurrence
Small transformation of
$$n!=n\times (n-1)!$$
gives
$$(n-1)!=\frac{n!}{n}$$
Substituting n = 1
$$(1-1)!=\frac{1!}{1}$$
$$0!=1!=1$$
This explanation, although easy, does not provide (in my opinion) deep enough understanding of “why this should be the best option”.
⭐️ Factorial n! counts the possible distinct sequences of n distinct objects (permutations)
Let’s assume we have a set containing n elements
$$\{1,2,\ldots,n\}$$
Now let”s count possible ordering of elements is this set
- n ways of selecting first element (because we have the whole set available)
- n-1 ways of selecting second element (because the first was already selected, there are n-1 left)
- n-2 ways of selecting third element (because the two were already selected, there are n-2 left)
- …
- n- (k-1) ways of selecting element number k (because the k-1 were already selected, n- (k-1) remain)
- 2 ways of selecting element number n-1 (because the n-2 were selected, still 2 remain)
- 1 way of selecting element number n (because the n-1 were were selected, remained only one)
Finally, counting all possible ways, we get
$$n\times (n-1)\times (n-2)\times \ldots \times 2\times 1=n!$$
Conclusion: Factorial of n counts the number of permutation of a set containing n elements.
⭐️ k-permutations of n sometimes called partial permutations or variations
The k-permutations of n are the different ordered arrangements of a k-element subset of an n-set. The number of such k-permutations of n is
$$P_k^n = n\times (n-1)\times (n-2)\times\ldots\times \bigg(n-(k-1)\bigg) = \frac{n!}{(n-k)!}$$
It is easy to see that n-permutation of n is a permutation, so
$$P_n^n=n!$$
$$n! = \frac{n!}{(n-n)!} = \frac{n!}{0!}$$
The next insight why 0!=1 is the correct definition comes from that for any n > 0 we should have
$$0! \times n! = n!$$
⭐️ Function as a sets mapping
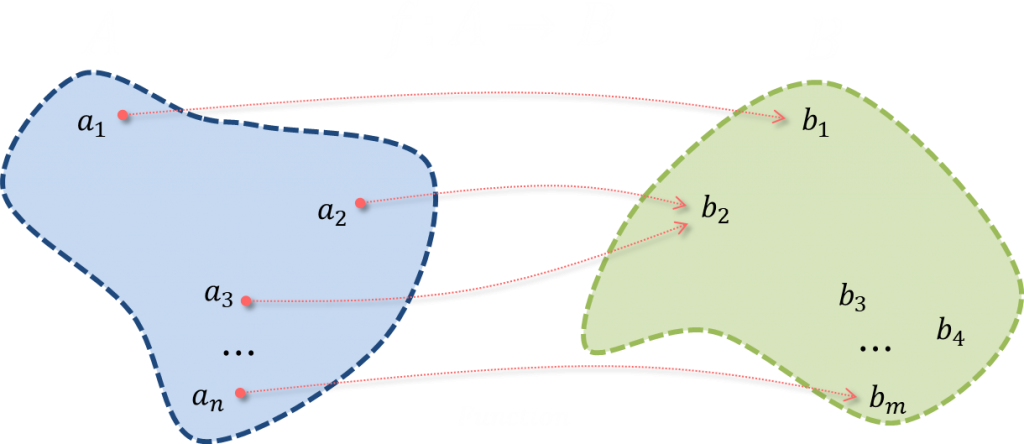
Function
$$f:A\to B$$
Function f : A → B, where for every a ∈ A there is f(a) = b ∈ B, defines the relationship between elements a and b. We can say that the elements a ∈ A and b ∈ B are in relation “f” if and only if f(a) = b.
⭐️ Function as a subset of Cartesian product
Function is a binary relation, meaning function can be expressed a subset of a Cartesian product.
$$(a,b)\in f \subseteq A\times B \iff f(a)=b$$
⭐️ Injective function
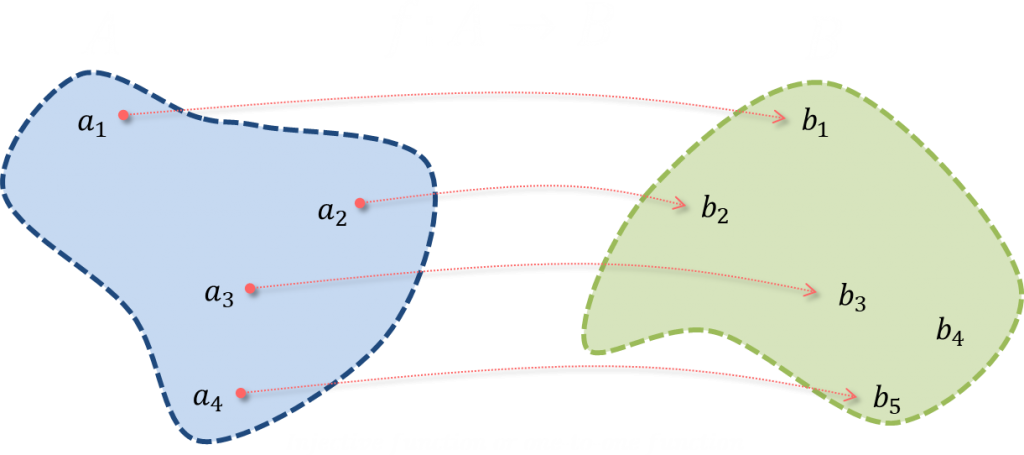
Injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. Shortly
$$x\neq y \Rightarrow f(x) \neq f(y)$$
⭐️ Surjective function
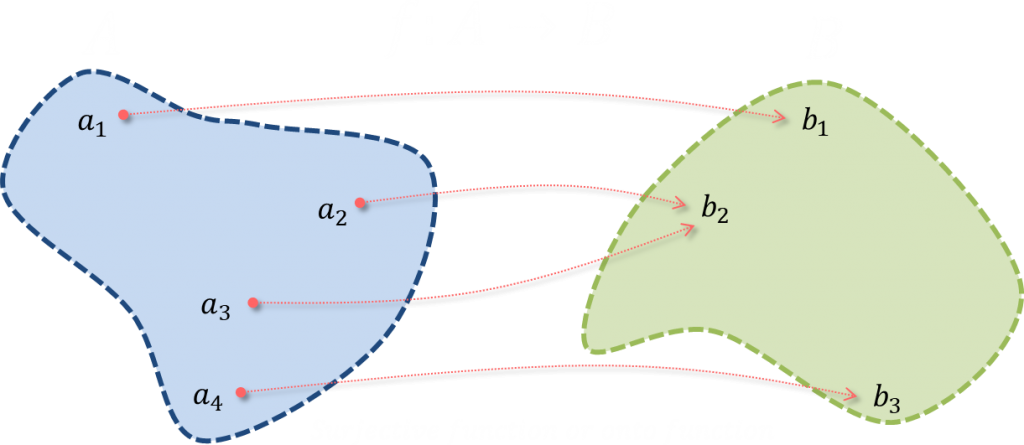
A function f is surjective (or onto) if for every element b in codomain, there is at least one element a in the domain such such that f(a)=b . It is not required that x be unique.
$$f:A\to B$$
$${\large \displaystyle\forall_{b \in B} \quad\displaystyle\exists_{a\in A}\quad}f(a)=b$$
⭐️ Bijective function
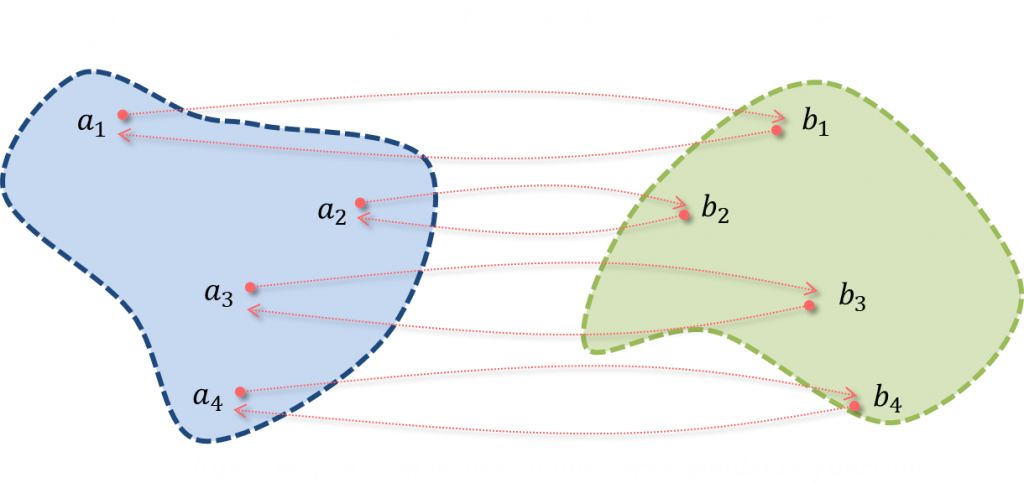
Bijective function, or one-to-one correspondence, is a function where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements.
In mathematical terms, a bijective function is both injective and surjective mapping of a set A to a set B.
⭐️ Bijective function vs Permutation
Permutation is a function that returns the order of a set, i.e. if we consider the n-element set {1, 2, …, n} then permutation will be a function
$$p:\{1, 2, …, n\}\to\{1, 2, …, n\}$$
satisfying the bijective function condition.
By asking about the number of permutations we can equally ask about the number of different bijections from a given set into itself.
⭐️ Empty function
An empty function is every function whose domain is an empty set.
$$f:\emptyset\to B$$
The empty function “chart” is an empty set, as the Cartesian product of domain and codomain is empty.
$$\emptyset\times B = \emptyset$$
The empty function preserves distinctness (is injective), because in the domain (an empty set) there are no two different elements for which the value of the function is equal.
⭐️ A special case of an empty function
Let’s analyse the function that maps empty to empty set
$$f:\emptyset\to\emptyset$$
Such a function is a bijection because it is injective function (as shown above) and there is no element in codomain (the codomain is an empty set) that is not in relation to the elements in the domain.
Please note that there is exactly one such a bijection, which is a results of that the function is a subset of the Cartesian product of domain and codomain. In this case this is only one possible set.
$$f:\emptyset\to\emptyset$$
$$\emptyset\times\emptyset = \emptyset$$
The empty set has exactly one subset, which is the empty set – thus such a bijection is uniquely defined.
⭐️ 0! = 1 vs Empty function
I wrote above that the number of permutations of an n-element set equals the number of distinct bijective functions from this set into itself.
Following – the permutation of 0-element set corresponds to the bijection from an empty set into the empty set/
The special case of empty function is just 1 – and I presented the proof that there exists only one such a function 🙂
Pretty deep insight why 0! should by 1.
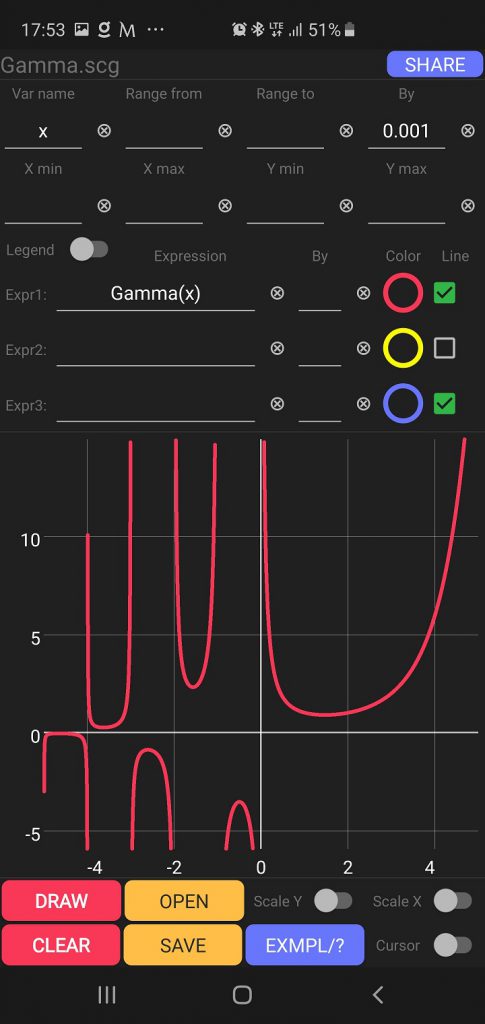
⭐️ The gamma function
In mathematics, the Gamma function is one of the extensions of the factorial function with its argument shifted down by 1, to real and complex numbers.
$$\Gamma(z)=\displaystyle\int_0^{+\infty}t^{z-1}e^{-t}dt$$
After integration by parts we get the recursive formula
$$\Gamma(z+1)=z\cdot\Gamma(z)$$
Let’s see the value of
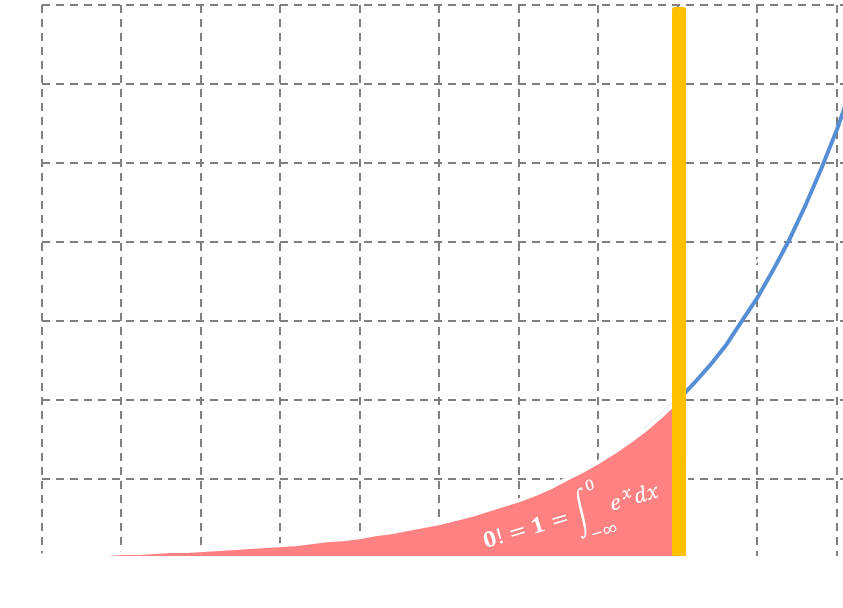
$$\Gamma(1)=?$$
$$\Gamma(1)=\displaystyle\int_0^{+\infty}e^{-t}dt=\displaystyle\int_{-\infty}^{0}e^{t}dt$$
Following
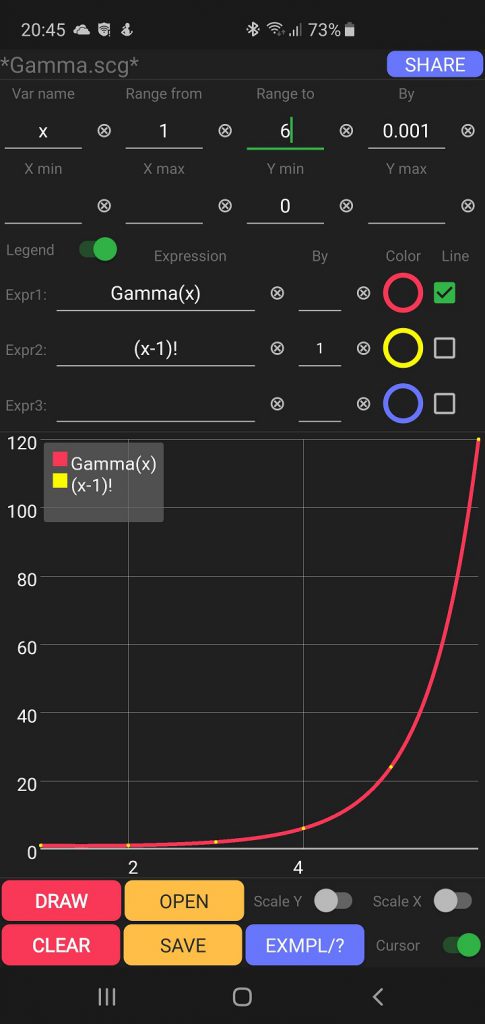
$$\Gamma(n+1)=n!$$
$$0! = \Gamma(1) = 1$$
⭐️ Scalar support for the Gamma function
Functions in Scalar Calculator, that support Gamma special function
- Gamma(x) – Gamma special function Γ(s)
- sgnGamma(x) – Signum of Gamma special function, Γ(s)
- logGamma(x) – Log Gamma special function, lnΓ(s)
- diGamma(x) – Digamma function as the logarithmic derivative of the Gamma special function, ψ(x)
- GammaL(s,x) – Lower incomplete gamma special function, γ(s,x)
- GammaU(s,x) – Upper incomplete Gamma special function, Γ(s,x)
- GammaP(s,x) , GammaRegL(s,x) – Lower regularized P gamma special function, P(s,x)
- GammaQ(s,x), GammaRegU(s,x) – Upper regularized Q Gamma special function, Q(s,x)
Gamma function chart
Gamma function vs Factorial chart
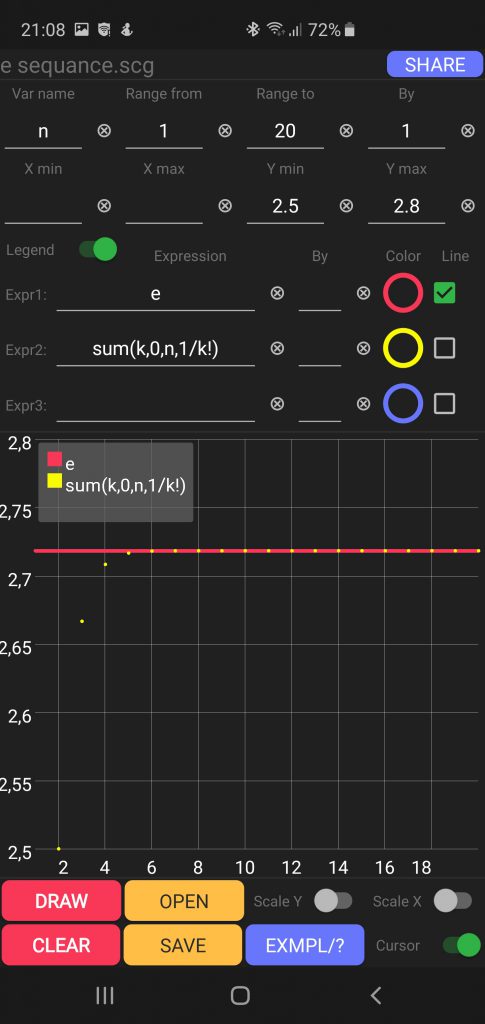
⭐️ Number e and factorial relation
Based on Taylor series expansion of e^x it is easy to show that
$$e=\displaystyle\sum_{n=0}^\infty\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots$$
Sequence convergence
This is fascinating, as it shows even stronger relation of factorial to e
Thanks for reading! All the best 🙂
? Scalar in action
? Scalar Lite (Free)

? Scalar Pro