✉️ Why is the area of a circle π·r² (pi r squared)?

$$A=\pi r^2$$

The above is perhaps the best known formula and is also rarely understood. Although the formula for the area of ​​a circle was already known in Ancient Greece, its justification is not easy at all. So it’s a great topic to enrich the “Why?” series.

⭐️ The area of a circle – formula

As you can see above – a square and a circle of the same area are not “somehow intuitively easy” related. Moreover, it has even been shown that squaring a circle (a procedure performed using a compass and a ruler without a scale) is impossible! And here comes the brilliant idea with a rectangle. Before I tell you what it is, let’s take a look at what the π·r² formula really says.

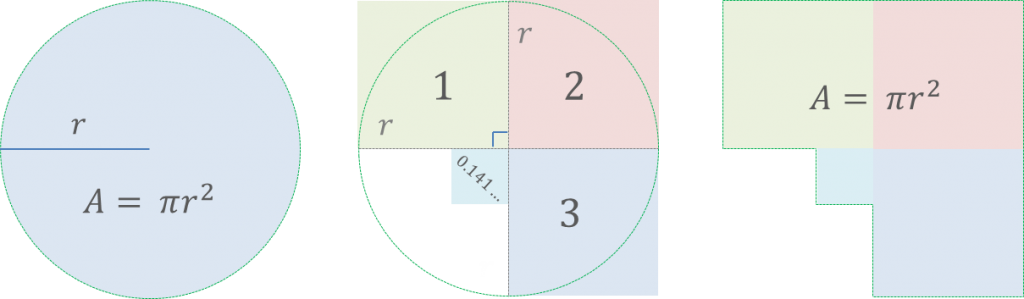
So there are slightly more than 3 squares of the side r in the circle with radius r.

⭐️ The area of a circle – proof by animation

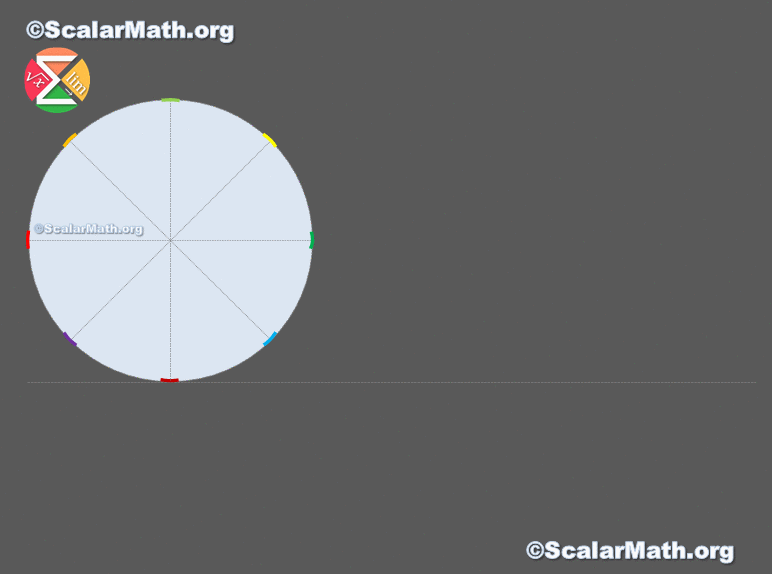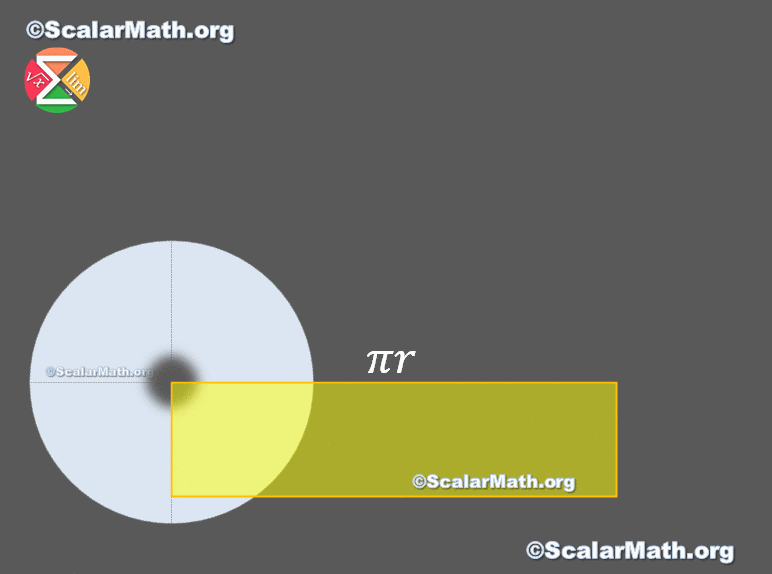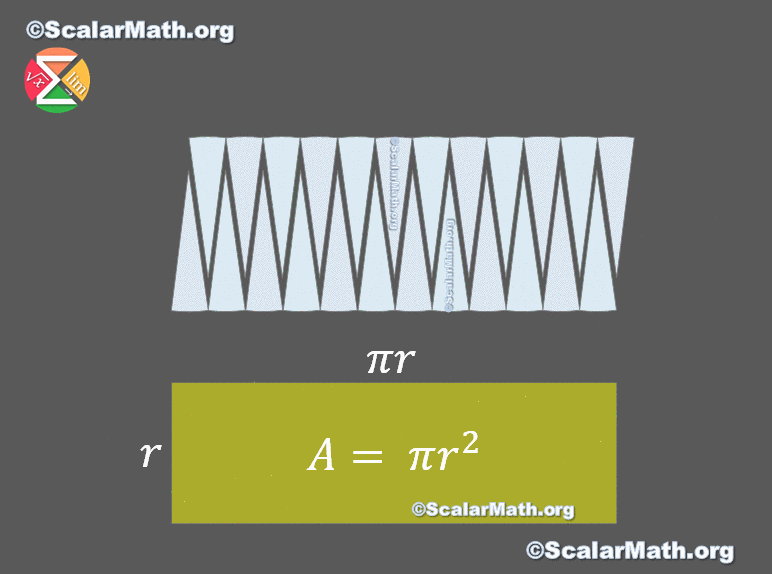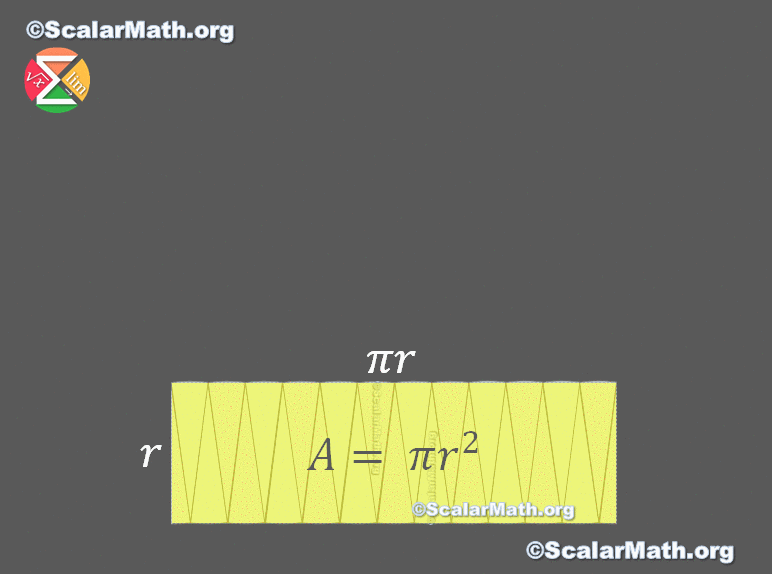
I worked hard on this animation, I hope you like it. Let me know in the comments 🙂

⭐️ The area of a circle – proof by regular polygons

Note – the following is not a formal proof, it only illustrates the inference method used by the Ancient Greeks (such as Archimedes’ and determination of the number pi).

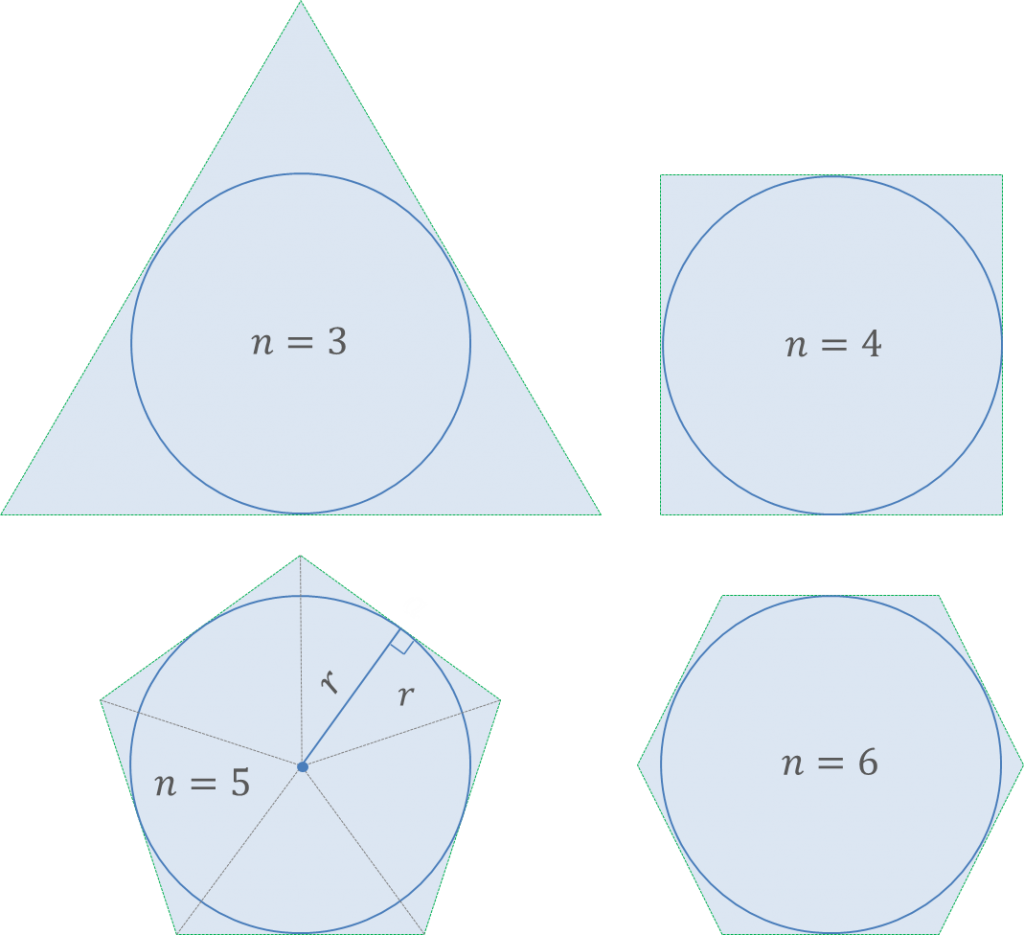
It can be seen that the circumference of the regular n-gon circumscribed on the circle is

$$C_n=na$$

and its area is the sum of the areas of the triangles with the base a and the height equal to the circle radius r.

$$A_n=n\frac{ar}{2}=\frac{nar}{2}$$

Substituting

$$A_n=\frac{C_nr}{2}$$

As n gets bigger, Aₙ approximates the circle’s area more and more closely, and Cₙ approximates its circumference. In the “limit step” (infinitesimal) we get the

$$C=\lim C_n=2\pi r$$

$$A=\lim A_n=\lim \frac{C_nr}{2}=\frac{r}{2}\lim C_n=…$$

$$…=\frac{r}{2}C=\frac{r}{2}2\pi r=\pi r^2$$

$$A=\pi r^2$$

⭐️ The area of a circle – a formal proof

The proof I am going to present will not be based on integrating the circle equation. I am going to use sequences and their limits and the squeeze theorem.

Squeeze theorem

Let be given three real sequences aₙ, bₙ, and cₙ. If “almost everywhere” (i.e. omitting at most finite many terms) there is a relation

$$a_n\leq b_n\leq c_n$$

and

$$\lim a_n = \lim c_n = g$$

then

$$\lim b_n = g$$

Useful limit

$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$

I remember from high school, in physics classes, my teacher repeatedly assumed that for small x the function sin (x) can be approximated well by x. It is a results of sin(x) expansion into the Taylor series – let me omit the explanation. However, I will calculate the limit using L’Hôpital’s rule. Later on it is going to be very useful 🙂

$$\lim_{x\to 0}\frac{\sin x}{x}=\big(\frac{0}{0}\big)\text{ L’Hôpital’s rule}=$$

$$=\lim_{x\to 0}\frac{(\sin x)\prime}{x\prime}=\lim_{x\to 0}\frac{\cos x}{1}=$$

$$=\frac{\cos 0}{1}=\frac{1}{1}=1$$

$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$

⭐️ The area of a circle – the proof

Let us consider regular n-gon circumscribed on a circle and inscribed inside a circle. Let us call “Outer area” the are of the circumscribed n-gon and denote it by Oₙ. Similarly, we will call the inscribed n-gon area as “Inner area”, marking it Iₙ.

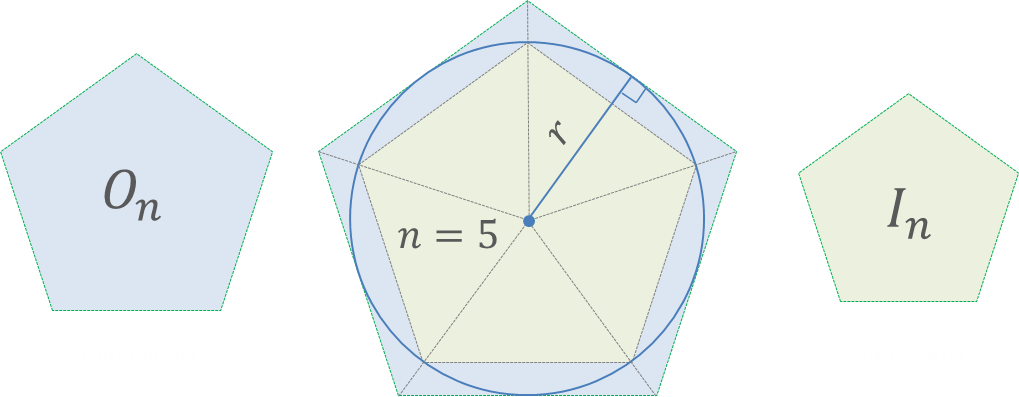
Obviously

$$I_n\leq A\leq O_n$$

where A states for the area of a circle.

In the next step, we divide n-gon into n-triangles. Note that in this way the full angle was also divided into n equal parts. The area of the “outer triangle” will be Tₙ and the area of the inner triangle tₙ.

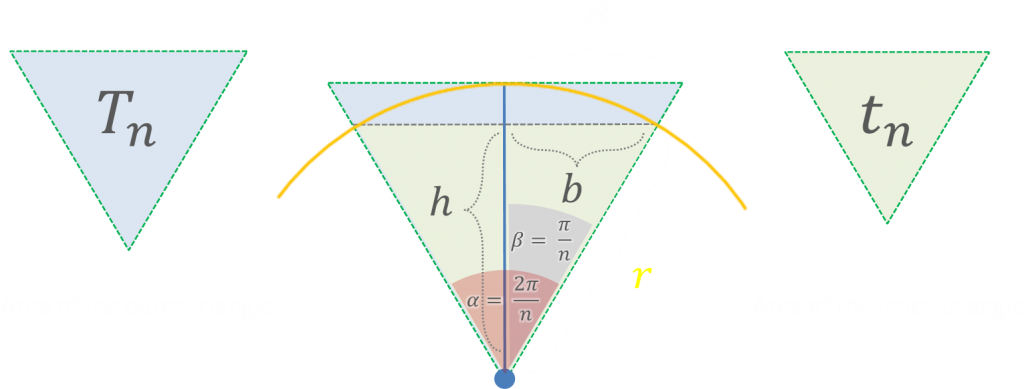
$$O_n=nT_n$$

$$I_n=nt_n$$

We determine the area of the “outer” triangle by

$$T_n=Br$$

but

$$\frac{B}{r}=\tan\beta=\frac{\sin\beta}{\cos\beta}$$

$$\frac{B}{r}r^2=r^2\frac{\sin\beta}{\cos\beta}$$

$$Br=r^2\frac{\sin\beta}{\cos\beta}$$

$$T_n=r^2\frac{\sin\beta}{\cos\beta}=r^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}$$

We determine the area of the “inner” triangle by

$$t_n=bh$$

but

$$\frac{b}{r}=\sin\beta$$

$$b=r\sin\beta$$

and

$$\frac{h}{r}=\cos\beta$$

$$h=r\cos\beta$$

substituting

$$t_n=r\sin\beta\cdot r\cos\beta=r^2\sin\beta\cos\beta$$

using trigonometric identities

$$t_n=r^2\sin\beta\cos\beta=\frac{r^2}{2}2\sin\beta\cos\beta=…$$

$$…=\frac{r^2}{2}\sin2\beta=\frac{r^2}{2}\sin\alpha$$

$$t_n=\frac{r^2}{2}\sin\alpha=\frac{r^2}{2}\sin\frac{2\pi}{n}$$

Final sequences

$$O_n=nT_n=nr^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}$$

$$I_n=nt_n=\frac{nr^2}{2}\sin\frac{2\pi}{n}$$

The limit of Oₙ ad Iₙ

$$\lim O_n=\lim nr^2\frac{\sin\frac{\pi}{n}}{\cos\frac{\pi}{n}}=$$

$$=\lim \frac{nr^2}{\cos\frac{\pi}{n}}\cdot\frac{\pi}{n}\cdot\frac{\sin\frac{\pi}{n}}{\frac{\pi}{n}}=$$

$$=\lim \frac{\pi r^2}{\cos\frac{\pi}{n}}\cdot\frac{\sin\frac{\pi}{n}}{\frac{\pi}{n}}=\frac{\pi r^2}{\cos 0}\cdot 1=$$

$$=\frac{\pi r^2}{1}=\pi r^2$$

$$\lim O_n=\pi r^2$$

$$\lim I_n=\lim\frac{nr^2}{2}\sin\frac{2\pi}{n}=$$

$$=\lim \frac{nr^2}{2}\cdot \frac{2\pi}{n}\cdot\frac{\sin\frac{2\pi}{n}}{\frac{2\pi}{n}}=$$

$$=\lim \pi r^2\cdot\frac{\sin\frac{2\pi}{n}}{\frac{2\pi}{n}}=\pi r^2\cdot 1=\pi r^2$$

$$\lim I_n=\pi r^2$$

Final conclusion

From the squeeze theorem we conclude that the area of the circle is

$$A=\lim O_n=\lim I_n=\pi r^2$$

⭐️ The convergence rate of the Oₙ and Iₙ sequences

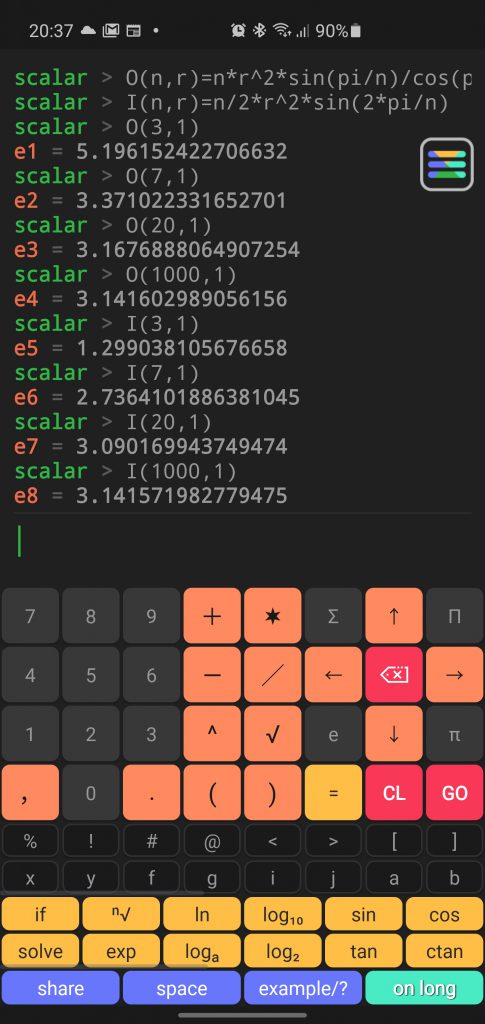
This is a perfect task for scalar calculator

scalar > O(n,r)=n*r^2*sin(pi/n)/cos(pi/n)
scalar > I(n,r)=n/2*r^2*sin(2*pi/n)
scalar > O(3,1)
e1 = 5.196152422706632
scalar > O(7,1)
e2 = 3.371022331652701
scalar > O(20,1)
e3 = 3.1676888064907254
scalar > O(1000,1)
e4 = 3.141602989056156
scalar > I(3,1)
e5 = 1.299038105676658
scalar > I(7,1)
e6 = 2.7364101886381045
scalar > I(20,1)
e7 = 3.090169943749474
scalar > I(1000,1)
e8 = 3.141571982779475

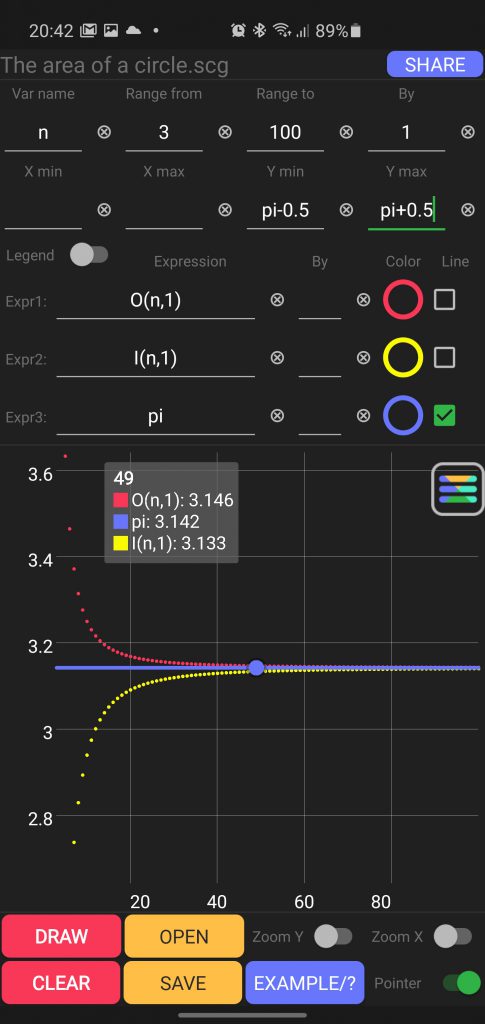
Plus the graph presenting sequences convergence

//The area of a circle.scg
var = n
from = 3
to = 100
miny = pi-0.5
maxy = pi+0.5
exp1 = O(n,1)
exp2 = I(n,1)
exp3 = pi
line1 = 0
line2 = 0
by = 1
curs = 1

Take care! Greetings.

? Scalar in Action

? Scalar Lite (Free)

? Scalar Pro