$$A=\pi r^2$$
The above is perhaps the best known formula and is also rarely understood. Although the formula for the area of a circle was already known in Ancient Greece, its justification is not easy at all. So it’s a great topic to enrich the “Why?” series.
⭐️ The area of a circle – formula

As you can see above – a square and a circle of the same area are not “somehow intuitively easy” related. Moreover, it has even been shown that squaring a circle (a procedure performed using a compass and a ruler without a scale) is impossible! And here comes the brilliant idea with a rectangle. Before I tell you what it is, let’s take a look at what the π·r² formula really says.
So there are slightly more than 3 squares of the side r in the circle with radius r.
⭐️ The area of a circle – proof by animation
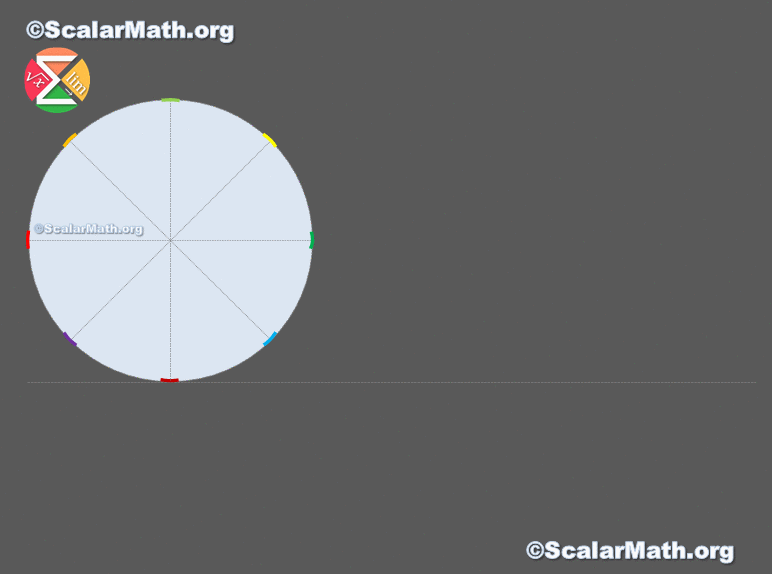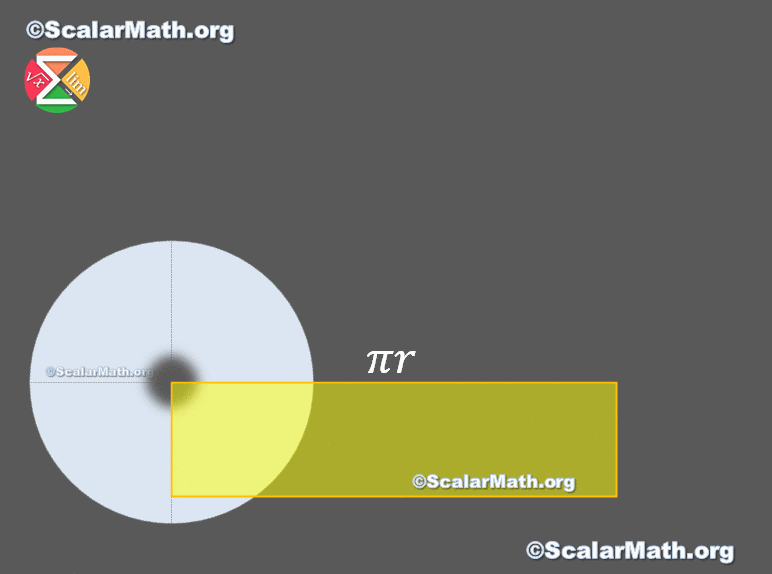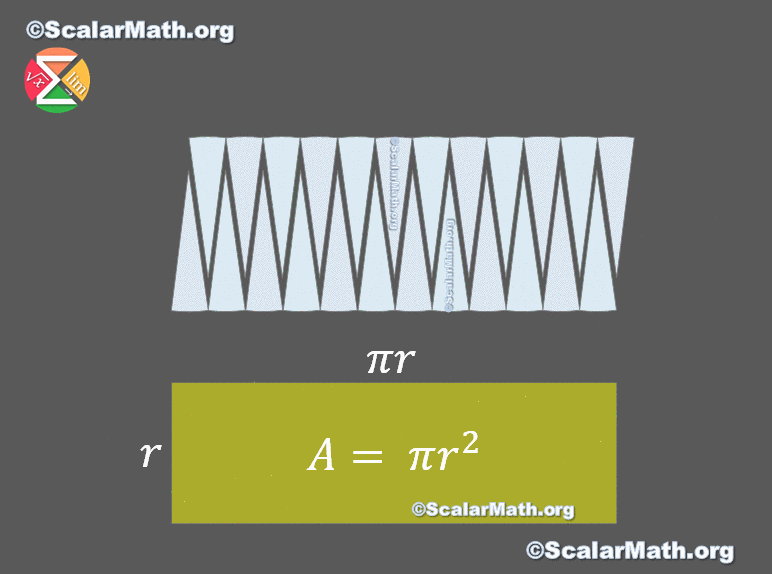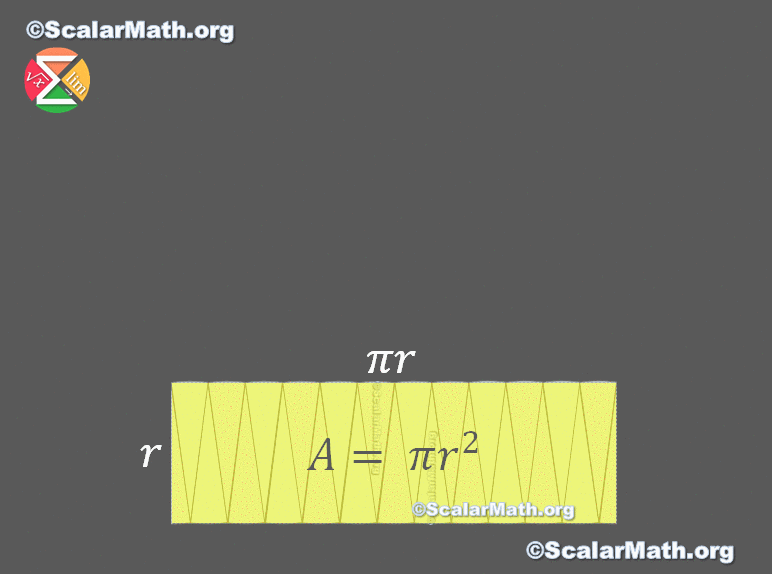
I worked hard on this animation, I hope you like it. Let me know in the comments 🙂
Continue reading “✉️ Why is the area of a circle π·r² (pi r squared)?”

