✉️ Why negative times a negative is a positive?

Surely everyone knows that the result of multiplying two negative numbers is positive. The formula “minus times a minus is a plus” or “negative times a negative is a positive” was put into our heads during the early school years. However, the teachers have forgotten to explain why this is the case, and to pass the motivation of mathematicians who defined the arithmetic of negative numbers.

⭐️ Multiplication as a short notation of repeated addition

It is said that multiplication is a short notation of repeated addition, which is absolutely true and, with a limitation to integers, a fairly obvious fact.

4 × 3 = 3 + 3 + 3 + 3 = 4 + 4 + 4 = 3 × 4 = 12

⭐️ The commutative property of multiplication and the distributive property of multiplication over addition

These two fundamental multiplication properties can be written as follows

commutative property: a × b = b × a

example: 3 × 4 = 4 × 3

distributive property: a × (b + c) = a × b + a × c

example: 3 × 4 = 3 × (1 + 3) = 3 × 1 +3 × 3 = 3 + 9 = 12

⭐️ Negative numbers multiplication from the mathematician point of view

Mathematicians, defining the arithmetic of negative numbers, wanted to be consistent with the already developed arithmetic of positive numbers and zero. Based on the interpretation of the short notation of repeated addition, we can easily justify the following:

−3 × 4 = (−3) + (−3) + (−3) + (−3) = −12

“By adding debt to debt,” we get more debt – intuitive. Now using the
commutative property of multiplication we get:

4 × (−3) = −3 × 4 = −12

At this point, the intuition is a bit more difficult, but the consistency has been preserved. Time to go to the main point – let’s try to answer the question:

−3 × (−4) = ?

To solve the above, we will use a trick based on the distributive property of multiplication over addition.

−3 × 0 = 0

−3 × 0 = −3 × (−4 + 4) = 0

−3 × (−4 + 4) = −3 × (−4) + (−3) × 4 = 0

−3 × (−4) + (−12) = 0

−3 × (−4) = 12

The above has nothing to do with intuition, but it is consistent, i.e. based on the arithmetic of positive numbers and zero, the commutative property of multiplication, the distributive property of multiplication over addition, we are able to justify why multiplying negative numbers must be a positive number.

⭐️ Multiplication of negative numbers as a reduction of loss

Suppose we multiply two numbers, where the interpretation of the first is the value of profit or losses, while the meaning of the second one is the multiplication (increase / decrease) of the first value. In this situation, multiplying two negative numbers means reducing the loss, ie the total positive effect of the action.

profit × increase = positive effect

profit × decrease = negative effect

loss × increase = negative effect

loss × decrease = positive effect

✅ The above explanation can be described as intuitive 🙂

Finally a video from Mathologer explaining the above problem (that was a base for the above post).

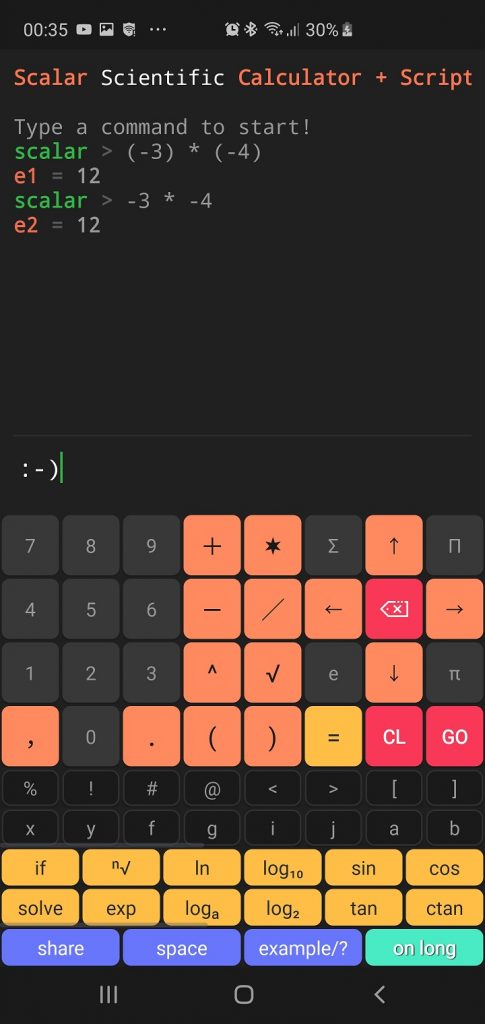
? Negative times a negative in Scalar Calculator? 🙂

Let’s run the negative numbers multiplication test using the Scalar calculator.

Test fully successful 🙂 Thank you for reading! All the best 🙂

? Scalar in action

? Scalar Lite (Free)

? Scalar Pro